Simple Linear Regression의 가장 큰 목표는 data들을 하나의 선으로 표현할 수 있는 선을 찾는 것이다.
Machine Learning을 공부해보면 가장 먼저 나오는 모델이라 볼 수 있다.
많은 곳에서 볼 수 있겠지만 가장 많이 보는 공식중 하나인

해당 공식은 machine learning상에서 w : weight , b : bias 라고 볼 수 있다
b가 있는 이유는 input이 아무것도 들어오지 않았어도 무엇인가 out put을 뱉기 위해 필요한 것

그림과 같이 붉은 색 점(학습을 위해 input한 데이터)들과의 거리가 가장 적은 직선을 구해야한다.
w와 b를 구하기 위한 공식으로 아래 공식과 같다.

1차원에서라면 해당 값을 구하는 것이 손으로 가능 하겠지만
다차원에서는 미분을 하는 것이 어렵기 때문에
Gradient descent라는 것을 사용해야 한다.(정확한 수치가 아닌 유사한 값을 구하기 위해)
그 다음 cost function의 값을 미분하여 b의 값을 만족하는 것을 찾아야한다.
- b로 미분
- w로 미분
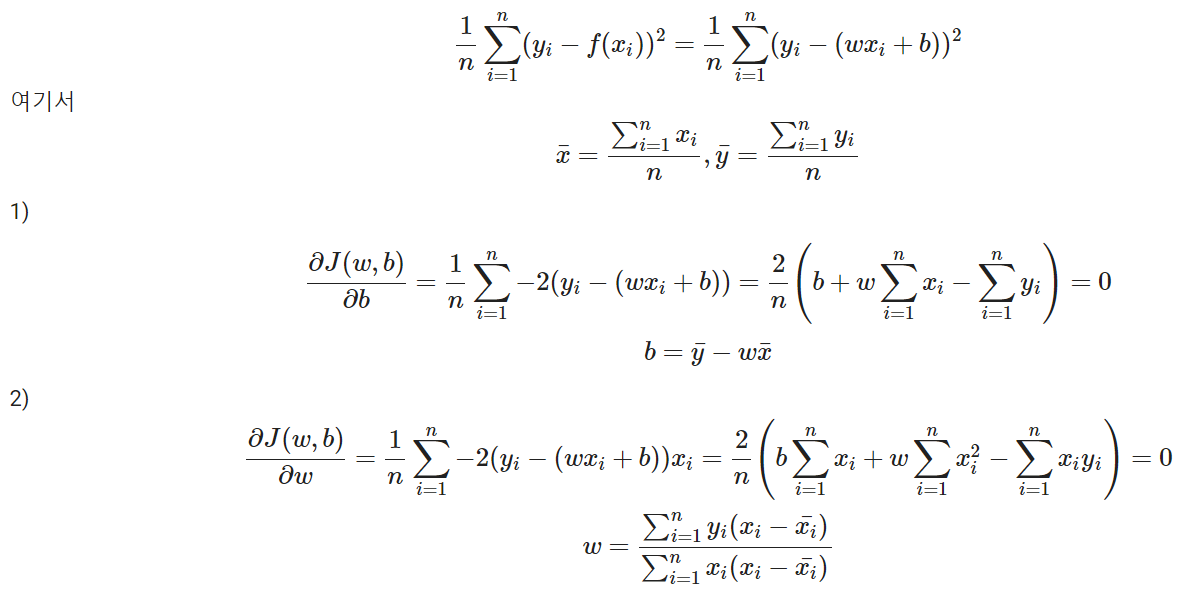
수식상으로 복잡하지만 코드로는 쉽게 구현이 가능하다.
import sympy
import numpy
from matplotlib import pyplot
%matplotlib inline
sympy.init_printing()
#-5,5사이의 값 100개
x_data = numpy.linspace(-5, 5, 100)
#임의의 w,b
w_true = 2
b_true = 20
#y = W*x + b
y_data = w_true*x_data + b_true + numpy.random.normal(size=len(x_data))
pyplot.scatter(x_data,y_data); #그래프 그리기임의의 데이터 그림 이 점들을 지나가는 하나의 선
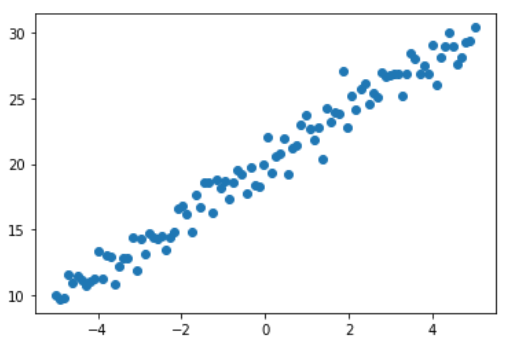
w, b, x, y = sympy.symbols('w b x y')
cost_function = (w*x + b - y)**2
#cost_function 대입
grad_b = sympy.lambdify([w,b,x,y], cost_function.diff(b), 'numpy')
grad_w = sympy.lambdify([w,b,x,y], cost_function.diff(w), 'numpy')
#w,b initalize
w = 0
b = 0
iteration = 1000
for i in range(iteration):
descent_b = numpy.sum(grad_b(w,b,x_data,y_data))/len(x_data)
descent_w = numpy.sum(grad_w(w,b,x_data,y_data))/len(x_data)
#w, b update
w = w - descent_w*0.01 # with 0.01 the step size
b = b - descent_b*0.01
pyplot.scatter(x_data,y_data)
pyplot.plot(x_data, w*x_data + b, '-r');
'Kaist 머신러닝 엔지니어 부트캠프 > Study' 카테고리의 다른 글
| Machine learning training 과정 (0) | 2022.05.19 |
|---|---|
| Logistic Regression (0) | 2022.05.18 |
| Numpy 관련 (0) | 2022.05.12 |
| Python 관련 (0) | 2022.05.12 |
| 딥러닝 최신 동향 (0) | 2022.05.09 |